El teorema fundamental de la hidrostática
¿Por qué las paredes de un dique van aumentando su espesor hacia el
fondo del lago? ¿Por qué aparecen las várices en las piernas?
Es un hecho experimental conocido que la presión en el seno de un
líquido aumenta con la profundidad. Busquemos una expresión matemática que nos
permita calcularla. Para ello, consideremos una superficie imaginaria horizontal
S, ubicada a una profundidad h como se muestra en la figura de la
derecha.
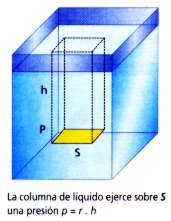
La presión que ejerce la columna de líquido sobre la superficie
amarilla será:
p = Peso del líquido/Area de la base
Con matemática se escribe: p = P/S = (d . V)/S=(d . S . h)/S= d . h (porque la S se simplifican)
donde p es el peso específico del líquido y V es el volumen de la
columna de fluido que descansa sobre la superficie S.
Es decir que la presión que ejerce un líquido en reposo depende del
peso específico (p) del líquido y de la distancia (h) a la superficie libre de
éste.
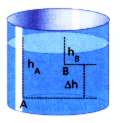 Si ahora
consideramos dos puntos A y B a diferentes profundidades de una columna de
líquido en equilibrio, el mismo razonamiento nos permite afirmar que la
diferencia de presión será:
Si ahora
consideramos dos puntos A y B a diferentes profundidades de una columna de
líquido en equilibrio, el mismo razonamiento nos permite afirmar que la
diferencia de presión será:
PA —PB = p . hA— d .
hB
Este resultado constituye el llamado teorema
fundamental de la hidrostática:
La diferencia de presión entre dos puntos dentro de una
misma masa líquida es el producto del peso específico del líquido por la
distancia vertical que los separa.
Ésta es la razón por la cual dos puntos de un fluido a igual
profundidad estarán a igual presión. Por el contrario, si la presión en ambos
puntos no fuera la misma, existiría una fuerza horizontal desequilibrada y el
líquido fluiría hasta hacer que la presión se igualara, alcanzando una situación
de equilibrio.
Hasta aquí sólo hemos encontrado la expresión de la presión que
ejerce el líquido sobre un cuerpo —imaginario o no— sumergido en una determinada
profundidad h. Ahora bien, ¿cuál es la presión total ejercida en el cuerpo? Si
tenemos en cuenta que, probablemente, por encima del líquido hay aire (que
también es un fluido), podemos afirmar que la presión total ejercida sobre el
cuerpo es debida a la presión de la columna del líquido más la presión que
ejerce el aire sobre la columna. Es decir:
P = Paire + Plíquido =
Patmosférica + d . h
Este resultado tiene generalidad y puede ser deducido del teorema
fundamental de la hidrostática. Veamos cómo. Si consideramos que el punto B se
encuentra exactamente en la superficie del líquido, la presión en A
es:
PA= PB+ d . Ah =
Psuperficie + P. (hA-hB) =
Patmosférica + d . h
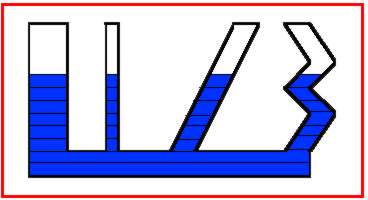
Los vasos comunicantes son recipientes comunicados entre sí,
generalmente por su base. No importa cuál sea la forma y el tamaño de los
recipientes; en todos ellos, el líquido alcanza la misma altura.
Cuando tenemos un recipiente vertical conteniendo un liquido
y le hacemos perforaciones en sus paredes, las emisiones del liquido de los
agujeros de la base tendrán mayor alcance que las emisiones de arriba, ya que a
mayor profundidad hay mayor presión.
EL
EMPUJE: PRINCIPIO DE ARQUÍMEDES
Resulta
evidente que cada vez que un cuerpo se sumerge en un líquido es empujado de
alguna manera por el fluido. A veces esa fuerza es capaz de sacarlo a flote y
otras sólo logra provocar una aparente pérdida de peso. Pero, ¿cuál es el origen
de esa fuerza de empuje? ¿De qué depende su intensidad?
Sabemos que
la presión hidrostática aumenta con la profundidad y conocemos también que se
manifiesta mediante fuerzas perpendiculares a las superficies sólidas que
contacta. Esas fuerzas no sólo se ejercen sobre las paredes del contenedor del
líquido sino también sobre las paredes de cualquier cuerpo sumergido en él.
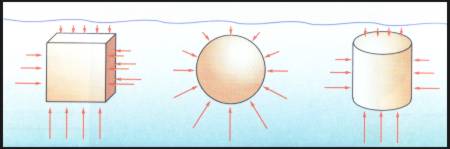
Distribución de las fuerzas sobre un cuerpo sumergido
Imaginemos
diferentes cuerpos sumergidos en agua y representemos la distribución de fuerzas
sobre sus superficies teniendo en cuenta el teorema general de la hidrostática.
La simetría de la distribución de las fuerzas permite deducir que la resultante
de todas ellas en la dirección lwrizontal será cero. Pero en la dirección
vertical las fuerzas no se compensan: sobre la parte superior de los cuerpos
actúa una fuerza neta hacia abajo, mientras que sobre la parte inferior, una
fuerza neta hacia arriba. Como la presión crece con la profundidad, resulta más
intensa la fuerza sobre la superficie inferior. Concluimos entonces que: sobre
el cuerpo actúa una resultante vertical hacia arriba que llamamos empuje.
Presión hidrostática:
 | Se define presión como el cociente entre la componente normal de la fuerza sobre una superficie y el área de dicha superficie. |
Absoluta, cuando se toma en cuenta la presión atmosférica.
Relativa, cuando no se toma en cuenta la presión atmosférica, en ingeniería se le denomina presión hidrostática.
Unitaria, cuando su intensidad se refiere a la unidad de area.
Total, cuando se refiere a toda una superficie y corresponde a la intensidad del empuje hidrostático.
Se mide en unidades de fuerza entre unidades de area (kg/m2, kg/cm2, lb/pie2 o derivadas).
Volumen
El volumen es una magnitud escalar definida como el espacio ocupado por un cuerpo. Es una función derivada ya que se halla multiplicando las tres dimensiones.
En matemáticas el volumen es una medida que se define como los demás conceptos métricos a partir de una distancia o tensor métrico.
En física, el volumen es una magnitud física extensiva asociada a la propiedad de los cuerpos físicos de ser extensos o materiales.
La unidad de medida de volumen en el Sistema Internacional de Unidades es el metro cúbico, aunque temporalmente también acepta el litro, que se utiliza comúnmente en la vida práctica.
En matemáticas el volumen es una medida que se define como los demás conceptos métricos a partir de una distancia o tensor métrico.
En física, el volumen es una magnitud física extensiva asociada a la propiedad de los cuerpos físicos de ser extensos o materiales.
La unidad de medida de volumen en el Sistema Internacional de Unidades es el metro cúbico, aunque temporalmente también acepta el litro, que se utiliza comúnmente en la vida práctica.
El volumen y la capacidad
La capacidad y el volumen son términos que se encuentran estrechamente relacionados. Se define la capacidad como el espacio vacío de alguna cosa que es suficiente para contener a otra u otras cosas. Se define el volumen como el espacio que ocupa un cuerpo. Por lo tanto, entre ambos términos existe una equivalencia que se basa en la relación entre el litro (unidad de capacidad) y el decímetro cúbico (unidad de volumen).Este hecho puede verificarse experimentalmente de la siguiente manera: si se tiene un recipiente con agua que llegue hasta el borde, y se introduce en él un cubo sólido cuyas aristas midan 1 decímetro (1 dm3), se derramará 1 litro de agua. Por tanto, puede afirmarse que:
- 1 dm3 = 1 litro
Unidades de volumen
Se clasifican de la siguiente manera en tres categorías:- Unidades de volumen sólido: Miden al volumen de un cuerpo utilizando unidades de longitud elevadas a la tercera potencia. Se le dice volumen sólido porque en geometría se utiliza para medir el espacio que ocupan los cuerpos tridimensionales, y se da por hecho que el interior de esos cuerpos no es hueco sino que es sólido.
- Unidades de volumen líquido. Estas unidades fueron creadas para medir el volumen que ocupan los líquidos dentro de un recipiente.
- Unidades de volumen de áridos, también llamadas tradicionalmente unidades de capacidad. Estas unidades fueron creadas para medir el volumen que ocupan las cosechas (legumbres, tubérculos, forrajes y frutas) almacenadas en graneros y silos. Estas unidades fueron creadas porque hace muchos años no existía un método adecuado para pesar todas las cosechas en un tiempo breve, y era más práctico hacerlo usando volúmenes áridos. Actualmente estas unidades son poco utilizadas porque ya existe tecnología para pesar la cosecha en tiempo breve.
Gasto másico
Gasto másico o Flujo másico es en física la magnitud que expresa la variación de la masa en el tiempo. Matemáticamente es la diferencial de la masa con respecto al tiempo. Se trata de algo frecuente en sistemas termodinámicos, pues muchos de ellos (tuberías, toberas, turbinas, compresores, difusores...) actúan sobre un fluido que lo atraviesa. Su unidad es el kg/s
Se puede expresar el flujo másico como la densidad ( , que puede estar en función de la posición,
, que puede estar en función de la posición, 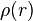 ) por un diferencial de volumen
) por un diferencial de volumen
Este volumen a su vez se puede expresar como el producto de una superficie S (el ancho de la tubería entrante, normalmente), que también puede depender de la posición por un diferencial de longitud (la porción de dicha tubería cuyo contenido entra en el sistema por unidad de tiempo).
o, integrando
Se puede expresar el flujo másico como la densidad (
 , que puede estar en función de la posición,
, que puede estar en función de la posición, 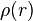 ) por un diferencial de volumen
) por un diferencial de volumen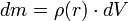 =
= 
Este volumen a su vez se puede expresar como el producto de una superficie S (el ancho de la tubería entrante, normalmente), que también puede depender de la posición por un diferencial de longitud (la porción de dicha tubería cuyo contenido entra en el sistema por unidad de tiempo).
o, integrando
 = número de entradas
= número de entradas = número de salidas
= número de salidas
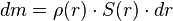

 = Gasto másico
= Gasto másico =
=  = Área del tubo corriente
= Área del tubo corriente





 en un punto
en un punto  en un instante dado dependen sólo de las deformaciones
en un instante dado dependen sólo de las deformaciones  en el mismo punto y no de las deformaciones anteriores (ni el valor de otras magnitudes en un instante anterior). Para un sólido elástico la
en el mismo punto y no de las deformaciones anteriores (ni el valor de otras magnitudes en un instante anterior). Para un sólido elástico la 
 denota el conjunto de tensores simétricos de segundo orden del espacio euclídeo. Si el sólido es homogéneo el valor de la función anterior no penderá del segundo argumento.
denota el conjunto de tensores simétricos de segundo orden del espacio euclídeo. Si el sólido es homogéneo el valor de la función anterior no penderá del segundo argumento.


 es la gravedad (9,8 m/s2) y
es la gravedad (9,8 m/s2) y 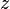 es la distancia del punto considerado a la superficie libre del líquido en reposo. En un fluido en movimiento la presión no necesariamente es isótropa, porque a la presión hidrostática se suma la
es la distancia del punto considerado a la superficie libre del líquido en reposo. En un fluido en movimiento la presión no necesariamente es isótropa, porque a la presión hidrostática se suma la 


