Equilibrio traslacional!!
Un cuerpo se encuentra en equilibrio traslacional cuando la sumatoria de todas las componentes en X es igual a 0 y todas las componentes en Y es igual a 0.
La línea de acción de un a fuerza es aquella línea imaginaria que se prolonga a lo largo del vector en los dos sentidos y por la cual se puede desplazar la fuerza sin alterar el efecto de la misma.
Cuando un cuerpo esta en equilibrio traslacional no tiene fuerza resultante actuando sobre el.
Primera Ley de Equilibrio:
Un cuerpo se encuentra en equilibrio si y sólo si la suma vectorial de las fuerzas que actúna sobre el es igual a 0.
Fx=Ax+Bx+Cx+Dx.......=0
Fy=Ay+By+Cy+Dy.......=0
Para resolver un problema de equilibrio traslacional de un cuerpo se deben seguir los siguientes pasos:
La línea de acción de un a fuerza es aquella línea imaginaria que se prolonga a lo largo del vector en los dos sentidos y por la cual se puede desplazar la fuerza sin alterar el efecto de la misma.
Cuando un cuerpo esta en equilibrio traslacional no tiene fuerza resultante actuando sobre el.
Primera Ley de Equilibrio:
Un cuerpo se encuentra en equilibrio si y sólo si la suma vectorial de las fuerzas que actúna sobre el es igual a 0.
Fx=Ax+Bx+Cx+Dx.......=0
Fy=Ay+By+Cy+Dy.......=0
Para resolver un problema de equilibrio traslacional de un cuerpo se deben seguir los siguientes pasos:
- Hacer un esquema del problema (dibujo)
- Realizar el diagrama de cuerpo libre de cada uno de los cuerpos, colocando todas las fuerzas que actúan en él.
- Plantear las ecuaciones de equilibrio traslacional para cada un o de los cuerpos.
- Resolver el sistema de ecuaciones obtenido
Ejemplo de Equilibrio rotacional y traslacional
Condiciones de equilibrio: Para que un cuerpo se encuentre en
equilibrio, se requiere que la sumatoria de todas las fuerzas o torcas
que actúan sobre él sea igual a cero. Se dice que todo cuerpo tiene dos
tipos de equilibrio, el de traslación y el de rotación.Traslación: Es aquel que surge en el momento en que todas las
fuerzas que actúan sobre el cuerpo se nulifican, o sea, la sumatoria de
las mismas sea igual a cero.
EFx = 0
EFy = 0
Rotación: Es aquel que surge en el momento en que todas las
torcas que actúan sobre el cuerpo sean nulas, o sea, la sumatoria de las
mismas sea igual a cero.
EMx= 0
EMy= 0
Aplicaciones: Se utiliza en todo tipo de instrumentos en los
cuales se requiera aplicar una o varias fuerzas o torques para llevar a
cabo el equilibrio de un cuerpo. Entre los instrumentos más comunes
están la palanca,la balanza romana, la polea, el engrane, etc.
EJEMPLO DE PROBLEMA DE APLICACIÓN:
Una caja de 8 N está suspendida por un alambre de 2 m que forma un
ángulo de 45° con la vertical. ¿Cuál es el valor de las fuerzas
horizontal y en el alambre para que el cuerpo se mantenga estático?.
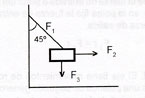
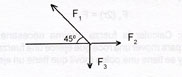
Primero se visualiza el problema de la siguiente manera:

A continuación se elabora su diagrama de cuerpo libre.

Ahora por medio de la descomposición de los vectores, calculamos la fuerza de cada uno de ellos.
F1x = - F1 cos 45°*
F1y = F1 sen 45°
F2x = F2 cos 0° = F2
F2y = F2sen0°=0
F3x = F3cos90°=0
F3y = - F3 sen 90° = - 8 N*
Porque los cuadrantes en los que se localizan son negativos.
Como únicamente conocemos los valores de F3, F2 y la sumatoria debe ser igual a cero en x e y, tenemos lo siguiente:
EFx=F1x+F2x+F3x=0
EFy=F1y+F2y+F3y=0
Por lo tanto tenemos lo siguiente:
EFx=-F1 cos 45+F2=0
F2=F1(0.7071)
EFy=-F1sen45-8N=0
8N=F1(0.7071)
F1=8N/0.7071=11.31 N
Para calcular F2, se sustituye F1 de la ecuación siguiente:
F2=F1(0.7071)
F2=11.31(0.7071)=8N

No hay comentarios:
Publicar un comentario